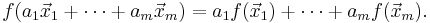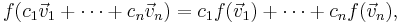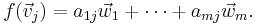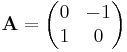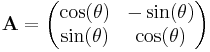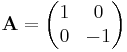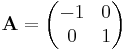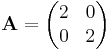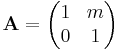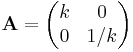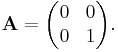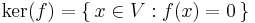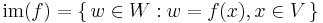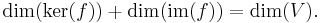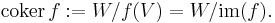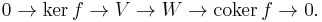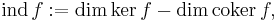Linear map
In mathematics, a linear map, linear mapping, linear transformation, or linear operator (in some contexts also called linear function) is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0.[1] The expression "linear operator" is commonly used for linear maps from a vector space to itself (i.e., endomorphisms). Sometimes the definition of a linear function coincides with that of a linear map, while in analytic geometry it does not.
In the language of abstract algebra, a linear map is a homomorphism of vector spaces. In the language of category theory it is a morphism in the category of vector spaces over a given field.
Definition and first consequences
Let V and W be vector spaces over the same field K. A function f : V → W is said to be a linear map if for any two vectors x and y in V and any scalar α in K, the following two conditions are satisfied:
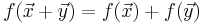 |
additivity |
 |
homogeneity of degree 1. |
This is equivalent to requiring the same for any linear combination of vectors, i.e. that for any vectors x1, ..., xm ∈ V and scalars a1, ..., am ∈ K, the following equality holds:
It immediately follows from the definition that f(0) = 0.
Occasionally, V and W can be considered to be vector spaces over different fields. It is then necessary to specify which of these ground fields is being used in the definition of "linear". If V and W are considered as spaces over the field K as above, we talk about K-linear maps. For example, the conjugation of complex numbers is an R-linear map C → C, but it is not C-linear.
A linear map from V to K (with K viewed as a vector space over itself) is called a linear functional.
Examples
- The identity map and zero map are linear.
- The map
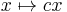 , where c is a constant, is linear.
, where c is a constant, is linear. - For real numbers, the map
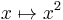 is not linear.
is not linear. - For real numbers, the map
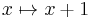 is not linear (but is an affine transformation, and also a linear function, as defined in analytic geometry.)
is not linear (but is an affine transformation, and also a linear function, as defined in analytic geometry.) - If A is a real m × n matrix, then A defines a linear map from Rn to Rm by sending the column vector x ∈ Rn to the column vector Ax ∈ Rm. Conversely, any linear map between finite-dimensional vector spaces can be represented in this manner; see the following section.
- The (definite) integral is a linear map from the space of all real-valued integrable functions on some interval to R
- The (indefinite) integral (or antiderivative) is not considered a linear transformation, as the use of a constant of integration results in an infinite number of outputs per input.
- Differentiation is a linear map from the space of all differentiable functions to the space of all functions.
- If V and W are finite-dimensional vector spaces over a field F, then functions that send linear maps f : V → W to dimF(W)-by-dimF(V) matrices in the way described in the sequel are themselves linear maps.
- The expected value of a random variable X is linear, as
![E[cX %2B a] = cE[X] %2B a](/2012-wikipedia_en_all_nopic_01_2012/I/bbc150c0ba4e1ff16e3663727740c16d.png) , but the variance of a random variable is not linear, as it violates the second condition, homogeneity of degree 1:
, but the variance of a random variable is not linear, as it violates the second condition, homogeneity of degree 1: ![V[cX %2B a] = c^2V[X]](/2012-wikipedia_en_all_nopic_01_2012/I/409a649c36be685e587aac570bfd8b56.png) .
.
Matrices
If V and W are finite-dimensional, and one has chosen bases in those spaces, then every linear map from V to W can be represented as a matrix; this is useful because it allows concrete calculations. Conversely, matrices yield examples of linear maps: if A is a real m-by-n matrix, then the rule f(x) = Ax describes a linear map Rn → Rm (see Euclidean space).
Let  be a basis for V. Then every vector v in V is uniquely determined by the coefficients
be a basis for V. Then every vector v in V is uniquely determined by the coefficients  in
in
If f : V → W is a linear map,
which implies that the function f is entirely determined by the values of 
Now let  be a basis for W. Then we can represent the values of each
be a basis for W. Then we can represent the values of each 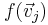 as
as
Thus, the function f is entirely determined by the values of 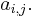
If we put these values into an m-by-n matrix M, then we can conveniently use it to compute the value of f for any vector in V. For if we place the values of  in an n-by-1 matrix C, we have MC = the m-by-1 matrix whose ith element is the coordinate of f(v) which belongs to the base
in an n-by-1 matrix C, we have MC = the m-by-1 matrix whose ith element is the coordinate of f(v) which belongs to the base 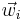 .
.
A single linear map may be represented by many matrices. This is because the values of the elements of the matrix depend on the bases that are chosen.
Examples of linear transformation matrices
In two-dimensional space R2 linear maps are described by 2 × 2 real matrices. These are some examples:
- rotation by 90 degrees counterclockwise:
- rotation by θ degrees counterclockwise:
- reflection against the x axis:
- reflection against the y axis:
- scaling by 2 in all directions:
- horizontal shear mapping:
- squeeze mapping:
- projection onto the y axis:
Forming new linear maps from given ones
The composition of linear maps is linear: if f : V → W and g : W → Z are linear, then so is their composition g o f : V → Z. It follows from this that the class of all vector spaces over a given field K, together with K-linear maps as morphisms, forms a category.
The inverse of a linear map, when defined, is again a linear map.
If f1 : V → W and f2 : V → W are linear, then so is their sum f1 + f2 (which is defined by (f1 + f2)(x) = f1(x) + f2(x)).
If f : V → W is linear and a is an element of the ground field K, then the map af, defined by (af)(x) = a (f(x)), is also linear.
Thus the set L(V,W) of linear maps from V to W itself forms a vector space over K, sometimes denoted Hom(V,W). Furthermore, in the case that V=W, this vector space (denoted End(V)) is an associative algebra under composition of maps, since the composition of two linear maps is again a linear map, and the composition of maps is always associative. This case is discussed in more detail below.
Given again the finite-dimensional case, if bases have been chosen, then the composition of linear maps corresponds to the matrix multiplication, the addition of linear maps corresponds to the matrix addition, and the multiplication of linear maps with scalars corresponds to the multiplication of matrices with scalars.
Endomorphisms and automorphisms
A linear transformation f : V → V is an endomorphism of V; the set of all such endomorphisms End(V) together with addition, composition and scalar multiplication as defined above forms an associative algebra with identity element over the field K (and in particular a ring). The multiplicative identity element of this algebra is the identity map id : V → V.
An endomorphism of V that is also an isomorphism is called an automorphism of V. The composition of two automorphisms is again an automorphism, and the set of all automorphisms of V forms a group, the automorphism group of V which is denoted by Aut(V) or GL(V). Since the automorphisms are precisely those endomorphisms which possess inverses under composition, Aut(V) is the group of units in the ring End(V).
If V has finite dimension n, then End(V) is isomorphic to the associative algebra of all n by n matrices with entries in K. The automorphism group of V is isomorphic to the general linear group GL(n, K) of all n by n invertible matrices with entries in K.
Kernel, image and the rank-nullity theorem
If f : V → W is linear, we define the kernel and the image or range of f by
ker(f) is a subspace of V and im(f) is a subspace of W. The following dimension formula is known as the rank-nullity theorem:
The number dim(im(f)) is also called the rank of f and written as rank(f), or sometimes, ρ(f); the number dim(ker(f)) is called the nullity of f and written as null(f) or ν(f). If V and W are finite-dimensional, bases have been chosen and f is represented by the matrix A, then the rank and nullity of f are equal to the rank and nullity of the matrix A, respectively.
Cokernel
A subtler invariant of a linear transformation is the cokernel, which is defined as
This is the dual notion to the kernel: just as the kernel is a subspace of the domain, the co-kernel is a quotient space of the target. Formally, one has the exact sequence
These can be interpreted thus: given a linear equation 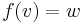 to solve,
to solve,
- the kernel is the space of solutions to the homogeneous equation
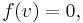 and its dimension is the number of degrees of freedom in a solution, if it exists;
and its dimension is the number of degrees of freedom in a solution, if it exists; - the co-kernel is the space of constraints that must be satisfied if the equation is to have a solution, and its dimension is the number of constraints that must be satisfied for the equation to have a solution.
The dimension of the co-kernel and the dimension of the image (the rank) add up to the dimension of the target space. For finite dimensions, this means that the dimension of the quotient space 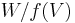 is the dimension of the target space minus the dimension of the image.
is the dimension of the target space minus the dimension of the image.
As a simple example, consider the map 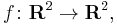 given by
given by 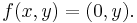 Then for an equation
Then for an equation 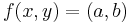 to have a solution, we must have
to have a solution, we must have 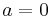 (one constraint), and in that case the solution space is
(one constraint), and in that case the solution space is 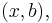 or equivalently stated,
or equivalently stated, 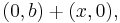 (one degree of freedom). The kernel may be expressed as the subspace
(one degree of freedom). The kernel may be expressed as the subspace 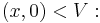 the value of x is the freedom in a solution – while the cokernel may be expressed via the map
the value of x is the freedom in a solution – while the cokernel may be expressed via the map 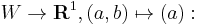 given a vector
given a vector 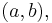 the value of a is the obstruction to there being a solution.
the value of a is the obstruction to there being a solution.
An example illustrating the infinite-dimensional case is afforded by the map 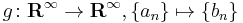 with
with 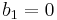 and
and 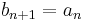 for
for 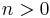 . Its image consists of all sequences with first element 0, and thus its cokernel consists of the classes of sequences with identical first element. Thus, whereas its kernel has dimension 0 (it maps only the zero sequence to the zero sequence), its co-kernel has dimension 1. Since the domain and the target space are the same, the rank and the dimension of the kernel add up to the same sum as the rank and the dimension of the co-kernel (
. Its image consists of all sequences with first element 0, and thus its cokernel consists of the classes of sequences with identical first element. Thus, whereas its kernel has dimension 0 (it maps only the zero sequence to the zero sequence), its co-kernel has dimension 1. Since the domain and the target space are the same, the rank and the dimension of the kernel add up to the same sum as the rank and the dimension of the co-kernel ( 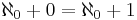 ), but in the infinite-dimensional case it cannot be inferred that the kernel and the co-kernel of an endomorphism have the same dimension (
), but in the infinite-dimensional case it cannot be inferred that the kernel and the co-kernel of an endomorphism have the same dimension (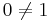 ). The reverse situation obtains for the map
). The reverse situation obtains for the map 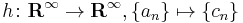 with
with 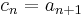 . Its image is the entire target space, and hence its co-kernel has dimension 0, but since it maps all sequences in which only the first element is non-zero to the zero sequence, its kernel has dimension 1.
. Its image is the entire target space, and hence its co-kernel has dimension 0, but since it maps all sequences in which only the first element is non-zero to the zero sequence, its kernel has dimension 1.
Index
For a linear operator with finite-dimensional kernel and co-kernel, one may define index as:
namely the degrees of freedom minus the number of constraints.
For a transformation between finite-dimensional vector spaces, this is just the difference 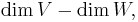 by rank-nullity. This gives an indication of how many solutions or how many constraints one has: if mapping from a larger space to a smaller one, the map may be onto, and thus will have degrees of freedom even without constraints. Conversely, if mapping from a smaller space to a larger one, the map cannot be onto, and thus one will have constraints even without degrees of freedom.
by rank-nullity. This gives an indication of how many solutions or how many constraints one has: if mapping from a larger space to a smaller one, the map may be onto, and thus will have degrees of freedom even without constraints. Conversely, if mapping from a smaller space to a larger one, the map cannot be onto, and thus one will have constraints even without degrees of freedom.
The index comes of its own in infinite dimensions: it is how homology is defined, which is a central theory in algebra and algebraic topology; the index of an operator is precisely the Euler characteristic of the 2-term complex 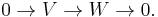 In operator theory, the index of Fredholm operators is an object of study, with a major result being the Atiyah–Singer index theorem.
In operator theory, the index of Fredholm operators is an object of study, with a major result being the Atiyah–Singer index theorem.
Algebraic classifications of linear transformations
No classification of linear maps could hope to be exhaustive. The following incomplete list enumerates some important classifications that do not require any additional structure on the vector space.
Let V and W denote vector spaces over a field, F. Let T:V → W be a linear map.
- T is said to be injective or a monomorphism if any of the following equivalent conditions are true:
- T is one-to-one as a map of sets.
- kerT = {0V}
- T is monic or left-cancellable, which is to say, for any vector space U and any pair of linear maps R:U → V and S:U → V, the equation TR=TS implies R=S.
- T is left-invertible, which is to say there exists a linear map S:W → V such that ST is the identity map on V.
- T is said to be surjective or an epimorphism if any of the following equivalent conditions are true:
- T is onto as a map of sets.
- coker T = {0W}
- T is epic or right-cancellable, which is to say, for any vector space U and any pair of linear maps R:W → U and S:W → U, the equation RT=ST implies R=S.
- T is right-invertible, which is to say there exists a linear map S:W → V such that TS is the identity map on W.
- T is said to be an isomorphism if it is both left- and right-invertible. This is equivalent to T being both one-to-one and onto (a bijection of sets) or also to T being both epic and monic, and so being a bimorphism.
- If T: V → V is an endomorphism, then:
- If, for some positive integer n, the n-th iterate of T, Tn, is identically zero, then T is said to be nilpotent.
- If T T = T, then T is said to be idempotent
- If T = k I, where k is some scalar, then T is said to be a scaling transformation or scalar multiplication map; see scalar matrix.
Change of basis
Given a linear map whose matrix is A, in the basis B of the space it transforms vectors coordinates [u] as [v]=A⋅[u]. As vectors change with the inverse of B, its inverse transformation is [v]=B⋅[v'].
Substituting this in the first expression:
![B \cdot [v'] = A \cdot B \cdot [u'] \rightarrow [v']=B^{-1}AB[u']](/2012-wikipedia_en_all_nopic_01_2012/I/e4cccb4f146940162a10b0d1d6b37141.png)
Therefore the matrix in the new basis is 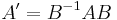 , being B the matrix of the given basis.
, being B the matrix of the given basis.
Therefore linear maps are said to be 1-co 1-contra -variant objects, or type (1, 1) tensors.
Continuity
A linear transformation between topological vector spaces, for example normed spaces, may be continuous. If its domain and codomain are the same, it will then be a continuous linear operator. A linear operator on a normed linear space is continuous if and only if it is bounded, for example, when the domain is finite-dimensional. An infinite-dimensional domain may have discontinuous linear operators.
An example of an unbounded, hence discontinuous, linear transformation is differentiation on the space of smooth functions equipped with the supremum norm (a function with small values can have a derivative with large values, while the derivative of 0 is 0). Differentiation is not a continuous operator; its codomain is larger than its domain, because the derivative of a smooth function need not be smooth.
Applications
A specific application of linear maps is for geometric transformations, such as those performed in computer graphics, where the translation, rotation and scaling of 2D or 3D objects is performed by the use of a transformation matrix.
Another application of these transformations is in compiler optimizations of nested-loop code, and in parallelizing compiler techniques.
See also
- Continuous linear operator
- wikibooks:Linear Algebra/Linear Transformations
- Neural network
- Computer graphics
References
- Halmos, Paul R. (1974), Finite-dimensional vector spaces, New York: Springer-Verlag, ISBN 978-0-387-90093-3
- Lang, Serge (1987), Linear algebra, New York: Springer-Verlag, ISBN 978-0-387-96412-6
|
|||||